Independent Component Analysis Clearly explained

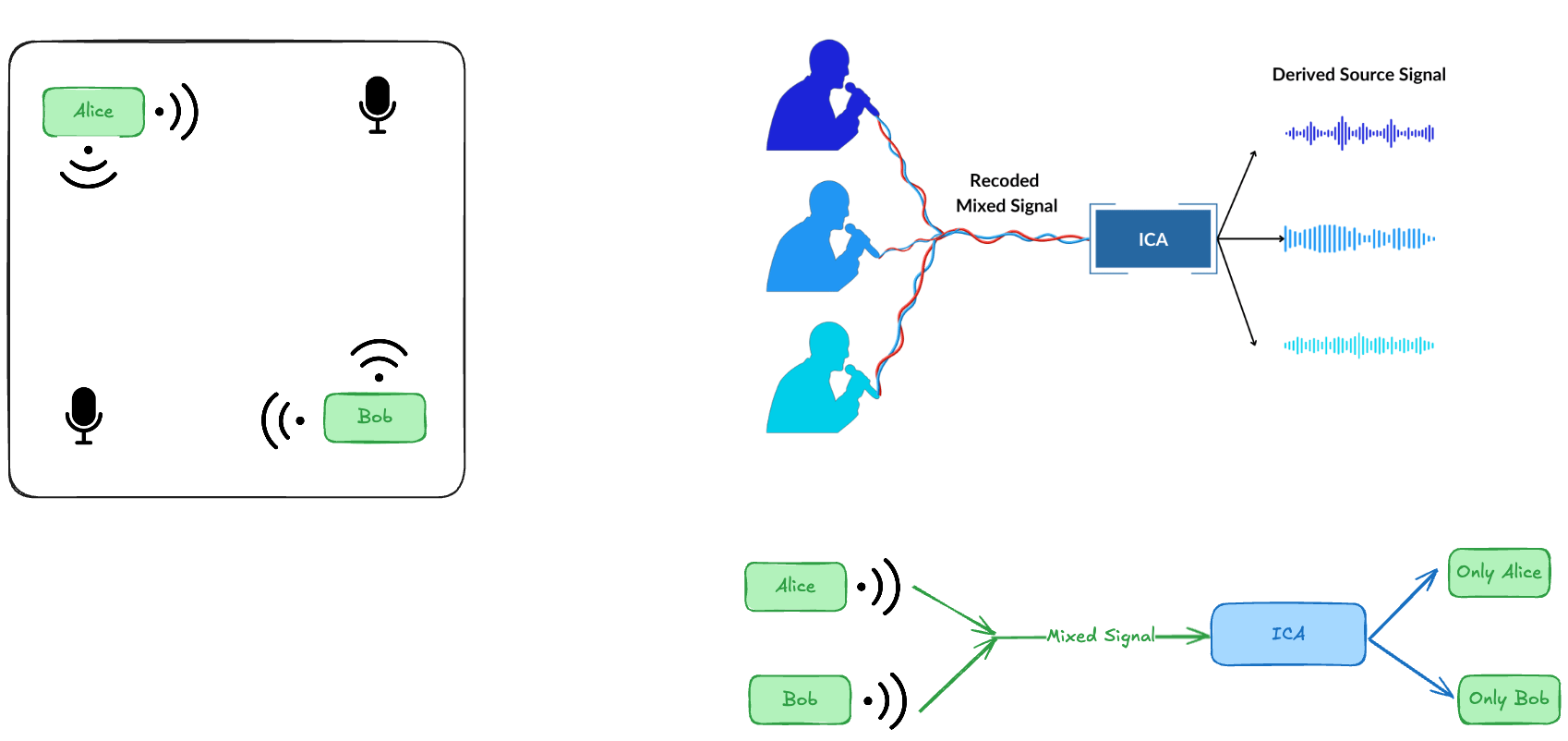
ICA is about separating mixed signals into their original, independent sources — even when you only observe mixtures.

Imagine you own a small café. In your café, two people are speaking:

• Alice is reading a book softly
• Bob is ranting about politics loudly

You, the café owner, place two microphones at different spots. Each microphone records both Alice and Bob mixed together. But with different mixtures (different volumes, angles).

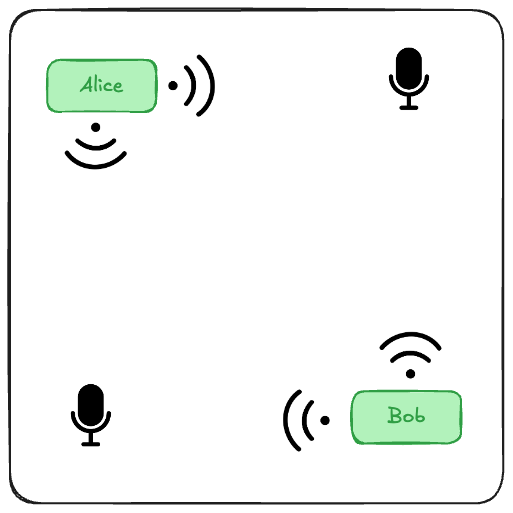
Result:

• Microphone 1: 70% Bob, 30% Alice
• Microphone 2: 40% Bob, 60% Alice

You have no idea who is speaking, or which voice is which. All you have are two messy recordings.

You want to take the two mixed recordings and separate them back into the original voices. This is the essence of Independent Component Analysis (ICA).

How ICA works, step-by-step

1. Assume: The original sources (Alice and Bob’s voices) are statistically independent. (What Alice says doesn’t depend on Bob.)
2. Observe: You only have access to the mixtures (the two microphone signals.)
3. Guess: Find a mathematical unmixing matrix that untangles the two voices.
4. Key idea: Pure sources (like individual voices) tend to have non-Gaussian shapes when you plot their amplitudes — whereas mixtures tend to look more like Gaussian noise. ICA looks for the most non-Gaussian projections.

Suppose:

$$\text{observed signals} = A \times \text{original signals}$$

Where:

• A = the unknown mixing matrix
• We know the observed signals and want to recover the original signals.

We find a matrix W (the unmixing matrix) such that:

$$\text{estimated sources} = W \times \text{observed signals}$$

The idea is to find W that makes the recovered signals as independent as possible

Tiny dummy example

Let’s say:

• Alice says numbers: $[1, 3, 2]$ (soft voice)
• Bob says numbers: $[7, 9, 6]$ (loud voice)

But microphones record:

Microphone 1	Microphone 2
4	6
6	8
4	6

(They heard mixtures.)

ICA would:

• Find a matrix that can unmix those and recover something like:
• First channel ≈ Alice
• Second channel ≈ Bob

Mathematically:

$$X = A \times S$$

Where:

• $X$ = observed mixtures (what microphones record)
• $S$ = true sources (the real voices)
• $A$ = unknown mixing matrix (how they got mixed)

You want to find W (the unmixing matrix) such that:

$$S = W \times X$$

and the rows of $S$ become as independent as possible.

Our inputs from earlier would be:

Time Step	Alice (S1)	Bob (S2)
1	1	7
2	3	9
3	2	6

We don’t hear these directly. Instead, microphones record mixtures:

Suppose the mixing matrix is:

$$A = \begin{bmatrix} 0.6 & 0.4 \\\\ 0.4 & 0.6 \end{bmatrix}$$

and the observed mixed signals are:

$$X = A \times S$$

To calculate X:

At time step 1:

$$\text{Mic 1} = 0.6(1) + 0.4(7) = 0.6 + 2.8 = 3.4$$ $$\text{Mic 2} = 0.4(1) + 0.6(7) = 0.4 + 4.2 = 4.6$$

At time step 2:

$$\text{Mic 1} = 0.6(3) + 0.4(9) = 1.8 + 3.6 = 5.4$$ $$\text{Mic 2} = 0.4(3) + 0.6(9) = 1.2 + 5.4 = 6.6$$

At time step 3:

$$\text{Mic 1} = 0.6(2) + 0.4(6) = 1.2 + 2.4 = 3.6$$ $$\text{Mic 2} = 0.4(2) + 0.6(6) = 0.8 + 3.6 = 4.4$$

And then we try to find W such that:

$$S = W \times X$$

ICA algorithms follow 3 main steps:

1. Centering: Subtract the mean from each signal to make them zero-mean.

$$\text{mean}(X1) = (3.4 + 5.4 + 3.6)/3 = 4.13$$ $$\text{mean}(X2) = (4.6 + 6.6 + 4.4)/3 = 5.2$$

Centered data:

Time Step	Mic 1 (X1 centered)	Mic 2 (X2 centered)
1	-0.73	-0.6
2	1.27	1.4
3	-0.53	-0.8

This step is important to remove biases.

2. Whitening: Make the variables uncorrelated and have variance 1. Whitening = standardizing + rotating.

For small examples we could skip this step to simplify. In reality: We compute the covariance matrix of the centered X, then apply a transformation so that:

$$\text{cov}(X_{\text{white}}) = I$$

3. Find directions of maximum non-Gaussianity

Rotate the whitened data. Search for directions that make the data most independent (least Gaussian).

How? Maximize kurtosis (peakedness) Or minimize mutual information between signals.

Technically: Solve for W by iterative optimization.

In a 2×2 case, the solution often looks like finding a rotation matrix that "untangles" the axes.

Suppose (for our simple example), the unmixing matrix W is found approximately as:

$$W = \begin{bmatrix} 1.5 & -1 \\\\ -1 & 1.5 \end{bmatrix}$$

Apply W to the centered X:

Calculate:

$$S = W \times (X - \text{mean})$$

You recover two clean rows:

• Row 1 ≈ Alice (softer signal)
• Row 2 ≈ Bob (louder signal)

And that’s it! You’ve separated the voices. This is a simplified example, but ICA works similarly in real-world applications.