Process Algebra

Imagine you are building a system for a vending machine for a train station that prints 2 different kinds of tickets: Children tickets, which are only 5€ and Adult tickets, which cost 10€. The vending machine takes only 5€ and 10€ bills. So if you want an adult ticket, you either need to put in 2x5€ or 1x10€.

We can simply sketch this process like this:

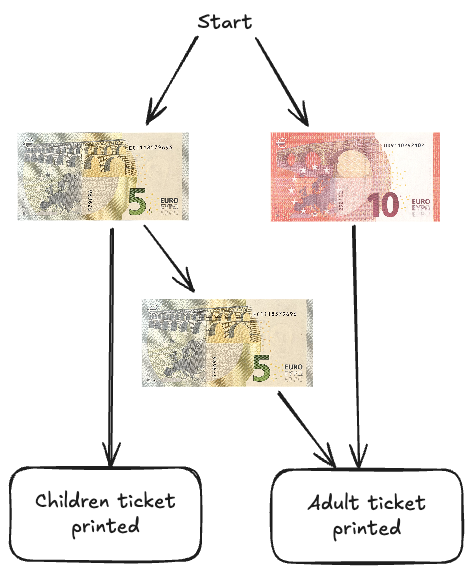
Now, we can actually model this using algebra. This is what we'll be talking about today.

"But why is this useful? I will probably never design Vending machine systems"

This is actually really important for modeling distributed and concurrent systems. Especially also for AI engineering this could be very important. Since we begin to add more and more LLM Agents into our systems, we need to make our systems concurrent. Learning the Algebraic basics of these systems helps not only in designing them, but also to find alternatives, compare different versions and prove if they will work or fail.

Rules

Syntax

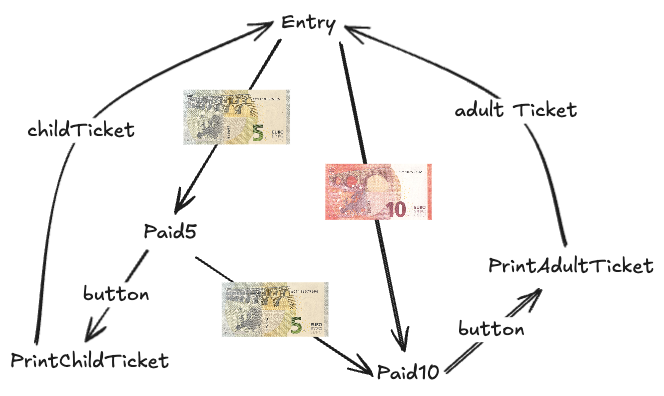
Now let's get back to the vending machine example. We can rewrite this system as such:

• $\text{Entry} = \text{5Euro.Paid5} + \text{10Euro.Paid10}$
• $\text{Paid5} = \text{button.childTicket.Print} + \text{5Euro.Paid10}$
• $\text{Paid10} = \text{button.adultTicket.Print}$

Now this looks a bit weird. So let's break it down.

• States: Entry, Paid5 and Paid10 refer to states. you can either be in the beginning, have paid 5 Euros or have paid 10 Euros
• $=$: The Equals operator show Processes are possible from a state. e.g. If you're in the Paid10 state, all you can do is print the ticket
• $+$: The + Operator just shows that these processes are concurrent. They are not dependent to each other.
• $.$: The dot operator (.) represents a sequence of actions. For example, in 5Euro.Paid5, inserting a 5€ bill leads to the Paid5 state.

With that said, let's redraw our diagram.

Operational Semantcs

Operational semantics gives you rules that say “if a process looks like this, then it can do that action and turn into that other process.” You can think of it as the little engine that tells you how your algebraic spec runs, step by step.

They look like this:

a.P means “do action a first, then behave like process P.”

The horizontal line with nothing above it means “this rule always applies”, there are no extra conditions.

Below the line is the conclusion: $a.P \xrightarrow{a} P$ reads “Process a.P can perform action a and then become P.”

a and P are called Meta variables. Where a is an action and P is a process.

Parameters

You can also add parameters to both actions and equations, just like functions. For our previous example, it could look like this:

• $P = euro(x).Paid(x)$
• $Paid(5) = button.print(childTicket).P + euro(5).Paid(10)$
• $Paid(10) = button.print(adultTicket).P$

This turns Process Algebra actually to a real programming language. (Which sounds super weird).

Edit: There are actually some languages based on Process Algebra, such as occam-pi. Never heard of it before but would be cool looking into in the future

Parallell processes

Process Algebra defines 2 parallell processes as such:

You take two processes, P and Q, and run them “side-by-side." -> They synchronize (must act together) on any action in the set Θ. -> They interleave independently on actions not in Θ.

But what is Θ? It's the Intersection between the sum of P with the sum of Q:

$$\Theta \;=\; \Sigma(P)\;\cap\;\Sigma(Q)$$

Example:

• If P can do $\mathsf{printChild},\mathsf{giveChange}$
• and Q can do $\mathsf{printChild},\mathsf{log}$,
• then $\Theta$ = $\mathsf{printChild}$

So if we define $R_{\parallel}$ as such:

$$\frac{P \xrightarrow{a} P{\prime} \quad Q \xrightarrow{a} Q{\prime} \quad a \in \Theta} {P \;\parallel_{\Theta}\; Q \;\xrightarrow{a}\; P{\prime} \;\parallel_{\Theta}\; Q{\prime}} \quad (R_{\parallel})$$

We would read it like this:

1. Above the line we list the premises—what must be true first:

• $P \xrightarrow{a} P{\prime}$ means “P can do action a and become $P{\prime}$.”
• $Q \xrightarrow{a} Q{\prime}$ means “Q can also do a and become $Q{\prime}$.”
• $a \in \Theta$ says this action is one of the shared ones.

2. Below the line is the conclusion:

$$P \parallel_{\Theta} Q \;\xrightarrow{a}\; P{\prime} \parallel_{\Theta} Q{\prime}$$

i.e. “When running in parallel, they must fire a together, and end up in the pair of successor states.”

"But what about actions that are not shared"?

If only one side can do an action $b \not\in \Theta$, it may do it “solo” and the other side just idles:

$$\frac{P \xrightarrow{b} P{\prime} \quad b \notin \Theta} {P \parallel_{\Theta} Q \;\xrightarrow{b}\; P{\prime} \parallel_{\Theta} Q} \quad \frac{Q \xrightarrow{b} Q{\prime} \quad b \notin \Theta} {P \parallel_{\Theta} Q \;\xrightarrow{b}\; P \parallel_{\Theta} Q{\prime}}$$

Web servers, database writes, AI-agent threads all run in parallel. That's why it's important to understand these systems in a formal setting.

Linking

linking (often called renaming) lets you take a “template” process and “plug in” different action names—just like you’d instantiate a function or template in code. Concretely.

E.g. If we have this: $P = a → b → c → P$

we can produce two fresh copies that behave the same except they use different labels:

• $P[x/b]$ replaces every occurrence of $b$ in $P$ with $x$.
• $P[y/b]$ replaces every $b$ with $y$.

But why rename/link?

2 Reasons really:

1. Instantiate templates: Just like we just saw, you can write a generic process and then just make new ones based on the template
2. Connect subsystems: Suppose you have a payment handler that signals paid when money arrives, and a printer that listens for paid. You can link them by renaming as such:

$$Pay = insertCoin → paid → STOP$$ $$Print = paid → printTicket → STOP$$ $$System = Pay[insertCoin/payment] ‖\{payment\}‖ Print$$

Here $Pay[insertCoin/payment]$ makes its internal insertCoin appear as payment so it synchronizes with Print.

Renaming Ruls

$$\quad(R_{[]}) \frac{P \xrightarrow{a} Q} {P[b/a] \xrightarrow{b} Q[b/a]}$$

• Above the line: if in the original process P you can do action a and go to Q,
• Below the line: then in the renamed process $P[b/a]$ you can do b and go to the renamed successor $Q[b/a]$.

Milner's Scheduler

This is a classical example.

You have $n$ worker processes $P_1, P_2, \dots, P_n$. Each worker:

1. starts its job ($a_i$),
2. does some hidden work ($z_i$),
3. finishes its job ($b_i$),
4. then loops back to wait for the next start.

You want a round-robin policy: first $P_1$ runs, then $P_2$, …, then $P_n$, then back to $P_1$, and so on—no skipping, no out of order.

First, ignore the subscripts and write a template process $P$:

$P = a \rightarrow z \rightarrow b \rightarrow P$

• $a$ = "start the job"
• $z$ = "do internal work" (invisible to the scheduler)
• $b$ = "finish the job"
• then repeat

We need $n$ copies, each with its own labels:

• For worker $i$, rename:
  • $a \mapsto a_i$,
  • $z \mapsto z_i$,
  • $b \mapsto b_i$.

Formally: $P_i \;=\; P[a_i/a,\; z_i/z,\; b_i/b].$

If you just ran $R = P_1 \;\parallel\; P_2 \;\parallel\;\dots\parallel\; P_n$ then all $P_i$ would be free to start, finish, or interleave in any order—which doesn't enforce the strict $1 \rightarrow 2 \rightarrow \dots \rightarrow n$ sequence.

To force the order, we wrap each $P_i$ in a small controller $Q_i$. The job of $Q_i$ is:

1. ask $P_i$ to start ($a_i$),
2. once $a_i$ fires, pass a token $x_i$ to the next controller $Q_{i+1}$,
3. wait for $P_i$ to finish ($b_i$),
4. then wait to receive the token $x_{i-1}$ from the previous controller,
5. loop.

In symbols, the generic proxy $Q$ (before plugging in names) has this shape:

$Q = a . x . b . y . Q$

• After doing $a$, it sends $x$.
• After doing $b$, it waits for $y$.
• Then repeats.

Now we make $n$ copies $Q_1,\dots,Q_n$ by renaming:

• $Q_1 = Q[a_1/a,\; x_1/x,\; b_1/b,\; x_n/y]$
• For $2 \leq i \leq n$: $Q_i = Q[a_i/a,\; x_i/x,\; b_i/b,\; x_{i-1}/y].$

Then we compose all $Q_i$ in parallel: $R = Q_1 \;\parallel\; Q_2 \;\parallel\;\dots\parallel\; Q_n.$

Because each $Q_i$:

• must synchronize on $x_i$ with $Q_{i+1}$,
• must synchronize on $y_i$ (which is really $x_{i-1}$) with $Q_{i-1}$,

the only legal order of events is:

1. $a_1$, $z_1$, $b_1$ (run job 1),
2. then $a_2$, $z_2$, $b_2$,
3. …,
4. $a_n$, $z_n$, $b_n$,
5. then back to $a_1$, etc.

An initial attempt used $Q = a.x.b.y.Q$ which forces "start → send token → finish → receive token." But that can deadlock if a finish ($b$) and the next start ($a$) collide.

The fixed version instead writes $Q = a.x.(\,b.y\;+\;y.b\,)\;.Q$ so after sending its token it can either:

• do $b$ then wait $y$, or
• wait $y$ then do $b$,

whichever comes first. This decoupling lets the "finish" of one job and the "start" of the next happen in any safe order without deadlock.