
Matrix operations in Typescript
I am currently studying AI at university (JKU) and struggling with motivation and consistency. My current interests lean more towards software development because I feel like I wouldn’t be productive in the AI industry. It often feels like I lack the skills to contribute meaningfully, and university isn’t adequately preparing me for work outside of academia.
In response, I decided to adopt a hands-on learning approach by implementing and coding almost everything I learn myself using TypeScript and Deno. Why TypeScript and Deno? Simply out of curiosity. This is not intended to be a serious project or open-source library—just public source. If, in some unlikely way, it turns out to be somewhat usable, I might reconsider its purpose. For now, the project exists purely as a learning exercise to deepen my understanding of machine learning and math concepts.
I’ll begin this project and this series with a simple implementation of matrices, in preparation for future modules (and also because I need to revisit Linear Algebra…)
Motivation
As someone who finds it difficult to stay motivated when learning math concepts, it was important for me to first understand the practical applications of matrix math.
In software engineering, matrices are used in:
- Computer Graphics: Transformations, projections, and animations.
- Game Development: Physics simulations and character animations.
- Image Processing: Images are essentially matrices of pixel data.
- Cryptography: Certain encryption algorithms use matrix operations.
In machine learning, matrices are foundational to almost everything. For example, datasets are often represented as matrices, where rows correspond to samples and columns represent features.
Here’s a dummy dataset:
| Feature 1 | Feature 2 | Feature 3 | Label |
|---|---|---|---|
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
Would be represented as:
Class outline
Before we begin implementing operations, we need to define a Matrix class. Programmatically, a matrix is simply an array of arrays. For example:
This can be represented in code as:
We can represent it in code as:
const matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9],
];
So we can define a class for matrices:
class Matrix {
public data: number[][];
constructor(data: number[][]) {
this.data = data;
}
}
For making it simpler in the future, we add private columns: number and private rows: number to the class. This way, we can easily calculate the number of columns and rows.
class Matrix {
public data: number[][];
private columns: number;
private rows: number;
constructor(data: number[][]) {
this.data = data;
this.columns = data[0].length;
this.rows = data.length;
}
}
Additionally, we will add a tuple to the class for the dimensions of the matrix. The logic for this goes like this:
Where the number of rows is the first number in the tuple and the number of columns is the second number in the tuple.
class Matrix {
public data: number[][];
private columns: number;
private rows: number;
private dimensions: [number, number];
constructor(data: number[][]) {
this.data = data;
this.columns = data[0].length;
this.rows = data.length;
this.dimensions = [this.rows, this.columns];
}
}
Printing the Matrix
I really wanted a nice way to print the matrix for debugging purposes. So I added my own pretty pring method. You don’t need to do this, but if you want to see it, you can look at in the github here.
The result of which looks like this in the terminal:
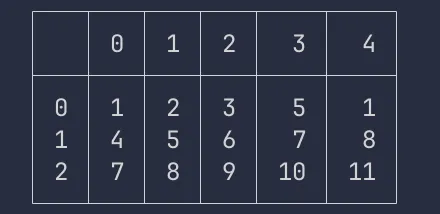
Matrix operations
Now we can conscentrate on the operations.
Addition and subtraction
For two matrices to be added, they must have the same dimensions. If they do, we can simply add the corresponding elements of the two matrices and return the result.
add(matrix: Matrix): Matrix {
// This is to check if the dimensions are the same
if (
this.dimensions[0] !== matrix.dimensions[0] ||
this.dimensions[1] !== matrix.dimensions[1]
) {
throw new Error("Matrices must have the same dimensions for addition.");
}
// Then we can do the actual addition
const newMatrix = new Matrix(
this.data.map((row, i) =>
row.map((value, j) => value + matrix.data[i][j]),
),
);
return newMatrix;
}
Similiarly for subtraction:
subtract(matrix: Matrix): Matrix {
if (
this.dimensions[0] !== matrix.dimensionsdimensions[0] ||
this.dimensions[1] !== matrix.dimensions[1]
) {
throw new Error("Matrices must have the same dimensions for subtraction.");
}
const newMatrix = new Matrix(
this.data.map((row, i) =>
row.map((value, j) => value - matrix.data[i][j]),
),
);
return newMatrix;
}
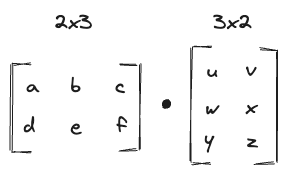
Dot product
The dot product of two matrices is defined as:
Where and are the matrices and and are the elements of the matrices.
However this seems like jibberish to me So to explain it better, I have prepared this graphic:
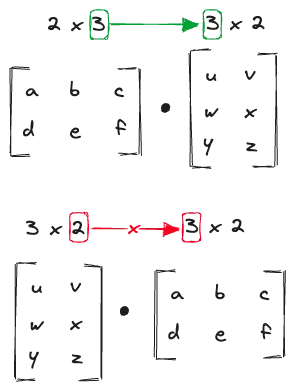
What is important before we begin the operation, is to check if the number of columns of the first matrix is the same as the number of rows of the second matrix. If they are not, we throw an error.
In code, this looks like this:
dot(matrix: Matrix): Matrix {
if (this.data[0].length !== matrix.data.length) {
throw new Error(
"Number of columns of the first matrix must equal the number of rows of the second matrix.",
);
}
}
The output dimensions of the dot product are the the number of rows of the first matrix and the number of columns of the second matrix.
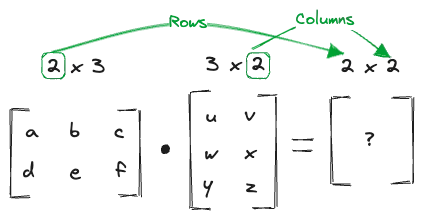
The actual operation, as mentioned above would look like this:
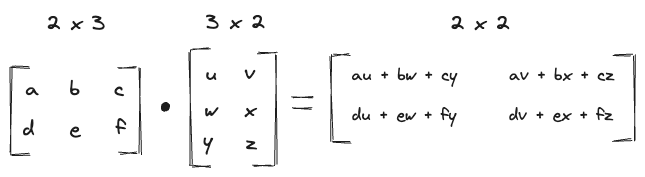
Implementing this in Typescript would look like this:
dot(matrix: Matrix): Matrix {
if (this.data[0].length !== matrix.data.length) {
throw new Error(
"Number of columns of the first matrix must equal the number of rows of the second matrix.",
);
}
const result = this.data.map((row, i) =>
matrix.data[0].map((_, j) =>
row.reduce((sum, value, k) => sum + value * matrix.data[k][j], 0),
),
);
return new Matrix(result);
}
This concludes the current set of operations. In future updates, I plan to implement additional functionality like transpose and determinant calculations.
